After binge eating for 3 days in a row (24-25-26 December), we switched to binge watching Netflix. Since we already had our good share of Christmas movies, we decided to start the second season of Squid Game.
It was pretty chilly outside and we needed to recharge our social batteries. So we didn’t just start the series, we ended up watching all the episodes in one day.
Several scenes reminded me of math, so I decided to make some computations. If you intend to watch the series and don’t want spoilers, you can take a look at some other posts.
Prize per player
456 people, with financial problems and desperate for money, take part to Squid Game: a series of contests with a potential jackpot of 45.6 billion won.
They realize, just too late, that if they fail in a contest they are killed. Indeed, for each death, the final prize increases by 100 million won. However, they get the chance after each round to decide, with a majority vote, to keep playing or stop and divide the prize among the contestants still alive.
After the second contest, many players start to consider the idea of “just another game” in order to win a larger sum while limiting the risk of death. Player 100 tries to convince many others to stay with the following words:
“It was 25 million after the first game and now it’s 78 million! After one game, the amount more than tripled! If we play one more game the prize would be at least 240 million!“
Using this populist slogan, he is hiding the fact that many people have to die in the next round. But how many?
The formula for computing the prize per person is $p = \dfrac{k \cdot D}{N-D}$ where $k$ is the sum added to the jackpot for each eliminated player, $D$ is the number of dead players and $N$ is the initial number of players.
Setting $N=456$ and $k=100$ million won, solving for $D$ we get D = 322. Given that at the end of second round the dead players were 201, this means 121 victims in round 3 out of 255. A little over 50% chance of surviving!
Here it’s a graph in log scale of the prize per person depending on the number of eliminated players
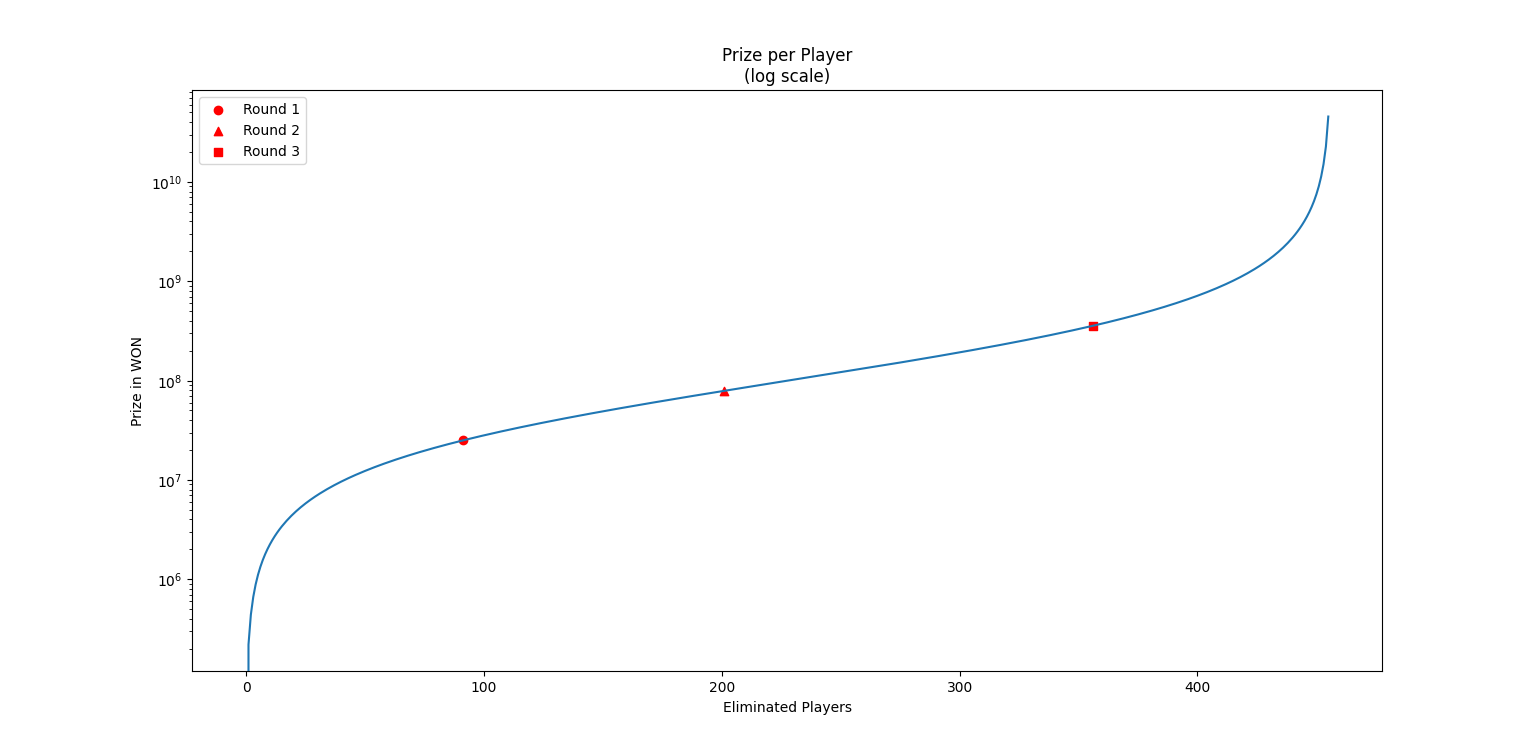
I had to use log scale otherwise the prize, over 400 eliminated players, would explode.
Now, let’s move the most interesting game from the statistical point of view, that by the way is not part of the actual games. It is indeed played with variations by one of the most recognizable characters of the show: the recruiter. He wanders in the Seoul underground stations looking for desperate people and proposing ddakji (traditional Korean game) matches where if he loses he gives money to the other player otherwise slaps him in the face. At the end of these exchanges, he leaves a business card to the person to enter the Squid Game.
Russian Roulette
Besides playing ddakji, the recruiter is fan of a riskier game: Russian Roulette.
All the scenes in which the recruiter plays (or makes others play) Russian Roulette are in episode 1.
Rock, Paper, Scissors Minus One
He starts by using it as a part of a particularly bloody game of Rock, Paper, Scissors Minus One that is in itself peculiar since you play with both hands Rock, Paper, Scissors and then you have to discard one.
The revolver is loaded with a bullet, and whoever loses the round gets a shot.
If you like statistics, you would probably ask yourself: what is the probability of losing forever the game? Defining $A$ as losing Rock, Paper, Scissors Minus One and $B$ as getting chamber with bullet this probability is $P(A, B)$.
The two events are independent, therefore $P(A, B) = P(A) \cdot P(B)$.
$P(A)$ depends on the number of chambers and the number of bullets. Therefore, $P(A) = \dfrac{bullets}{chambers}$. The number of chambers in the revolver is 6.
What about $P($losing Rock, Paper, Scissors Minus One$)$?
Ignoring, tendency of people to pattern matching and preferences of one item over the other, the probability of losing at traditional Rock, Paper, Scissors is $\dfrac{1}{3}$.
Rock, Paper, Scissors Minus One maintains the symmetry of the game, so instead of spending time (like I did) computing the 81 different cases, you can trust (or compute by yourself) that also for this version the probability of losing is still $\dfrac{1}{3}$.
By the way, I can tell you that playing with both hands the same item (if no strategy is involved) makes you win just $\dfrac{1}{9}$ of the times.
So the probability of getting killed when just one bullet is in the revolver is $\dfrac{1}{3} \cdot \dfrac{1}{6} = \dfrac{1}{18}$ roughly 5.5%. After some rounds the recruiter gets mad at the players keeping making ties so he adds 4 bullets to the revolver. In this case the probability of losing (not only the game) increases to $\dfrac{1}{3} \cdot \dfrac{5}{6} = \dfrac{5}{18}$: almost 28%!
No Reset
A few minutes later, Gi-hun (the main character) and the recruiter engage in a memorable confrontation, playing Russian Roulette with a twist: the revolver is spun only once at the start, therefore the odds don’t reset. This ensures that one of them will die after six rounds.
Apart from the fact that it is a crazy game, I thought: Is it better to be the first or the second to shoot?
The probability of losing the game is 50% since player 1 loses if the bullet is in chamber 1, 3, 5 and player 2 loses if in chamber 2, 4, 6.
This game without reset is particularly climax friendly since for each turn the probability of losing increases in a fatal way as $\dfrac{1}{6-n}$ where $n$ is the round number.
And guess what? Gi-hun is the first to play and the villain is second.
If you are interested in what happens with a different number of players StackExchange has got you covered.
Conclusions
For wrapping up what I learned watching and thinking about these episodes:
- looking 7 episodes longer than an hour in a day, it’s a little too much
- when playing Rock, Paper, Scissors Minus One is better not to play the same item with both hands (e.g. Rock and Rock)
- you should not trust a person proposing you to gamble in an underground station
- this season of Squid Game and upcoming season 3 should be together
- a paper was written to determine the best strategy to play Rock, Paper, Scissors but not rock was engraved and no scissors were sharpened
And after this last silly joke of 2024, it’s time for another dinner!